Compression Ratios and Speedups

I took a quick look at MonetDB/X100 – A DBMS In The CPU Cache recently.

MonetDB was the first database to optimize query execution for CPU caches¹, and there’s some interesting ideas to discuss there. But I want to take a closer look at a specific line of the paper. Before we get to that, let’s set up the context.

MonetDB achieved good execution times for in-memory workloads, but disk-based workloads were a challenge:

Due to its raw computational speed, MonetDB/X100 exhibits an extreme hunger for I/O bandwidth. As an extreme example, TPC-H Query 6 uses 216MB of data (SF=1)², and is processed in MonetDB/X100 in less than 100ms, resulting in a bandwidth requirement of ca. 2.5GB per second.

— Page 5 of the paper

First of all, what an interesting calculation! Surely I must have encountered it before, but I don’t think I was consciously aware of this technique to estimate I/O bandwidth requirements.

But ok, the main point is that there’s an I/O bottleneck now. The paper discusses three techniques here that will help:

1. “Decomposed Storage Model”, i.e. read only the columns you need³.
2. Compression, i.e. send more data using fewer bytes⁴.
3. “Cooperative Scans”, i.e. if another query is reading the same data that you need, reuse the data⁵. You can go further by scheduling queries so that queries operating on the same data get executed together. But you also need to avoid starving other queries.

On the topic of compression, the paper discusses the use of ultra lightweight compression:

Traditional compression algorithms usually try to maximize the compression ratio, making them too expensive for use in a DBMS.

— Page 5 of the paper

Makes sense. We’re trying to increase speed here, not compressing for compression’s sake⁶.

Now we get to one line that stumped me for a bit, which prompted this blog post. The line goes:

Preliminary experiments presented in Figure 5 show the speedup of the decompressed queries to be close to the compression ratio⁷, which in case of TPC-H allows for a bandwidth (and performance) increase of a factor of 3.

— Page 5 of the paper

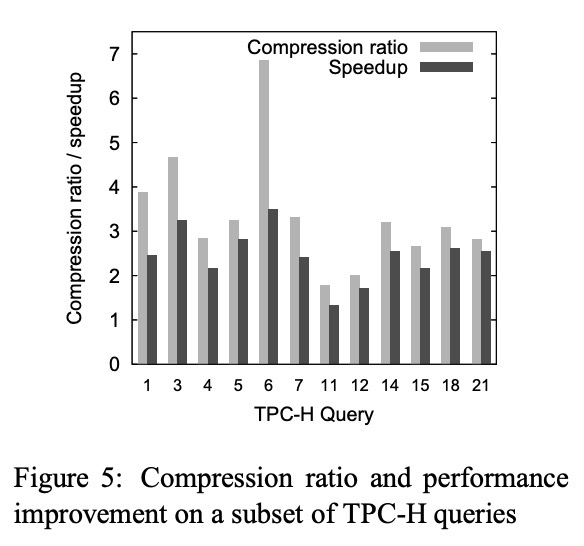
Why should I care that the compression ratio and speedups are similar? Shouldn’t I just care about speedup? Well…

We know that we’re currently I/O bound. This means that our CPU is processing data at the rate at which data is coming in.

Compression allows us to read more data per byte over our I/O devices. So the compression ratio gives us the multiplier for the new rate of incoming data, and thus the theoretical upper-bound speedup.

However, the system might not continue to be I/O bound. In the case of traditional compression algorithms, decompressing data might be so compute intensive that it eats up the theoretical speedup from an increased data bandwidth⁸.

Here’s the kicker. Although the paper says that speedup and decompressions being close is a good thing, what they mean more precisely⁹ is that the speedup being slightly lower than the compression ratio is a good thing.

There are three scenarios to consider here.

1. Speedup = Compression Ratio
2. Speedup <<< Compression Ratio
3. Speedup ≲ Compression Ratio

“Speedup = Compression Ratio” means that our workload remains data bandwidth bound. So we’re leaving speedups on the table when we should be increasing the compression ratio.

“Speedup <<< Compression Ratio” means that decompression is a significant bottleneck, and the high compression ratio is doing more harm than good.

“Speedup ≲ Compression Ratio” means that data bandwidth has just stopped being the bottleneck and decompression has just started being the bottleneck. Good job we found the perfect balance, and we’re getting all the theoretical speedups we can get from compression.

1. According to Wikipedia.
2. SF=1 refers to a scale factor of 1 which, for the TPC-H benchmark, refers to a 1GB database.
3. Brendan Gregg would call this “Don’t do it”. “It” being reading data for columns you don’t need.
4. “Do it cheaper”.
5. “Do it, but don’t do it again”.
6. If we were optimizing for storage costs this would be a different discussion.
7. They did a pretty bad job with TPC-H Q6 though :-)
8. It’s also possible that our execution engine simply isn’t fast enough, so even if data bandwidth increases and decompression is “free”, speedups might not increase as data bandwidth increases. This doesn’t really affect the discussion that follows because this scenario still implies that there is no further benefit to increasing compression ratio until our execution engine can keep up.
9. Maybe I’m being pedantic. When they said “close” I assume they were referring to the “equals” case, because the emphasis is on closeness. But a more charitable interpretation would be that they were referring to the “slightly lower” case. Either way, they could’ve been more precise.